Để chụp toàn cảnh, ta có thể sử dụng một gương hypebol. Máy ảnh được hướng về phía đỉnh của gương và tâm quang học của máy ảnh được đặt tại một tiêu điểm của gương (xem hình). Tìm khoảng cách từ quang tâm của máy ảnh đến đỉnh của gương, biết rằng phương trình cho mặt cắt của gương là \(\frac{x^{2}}{25}-\frac{y^{2}}{16}=1\).
Giải thích:
Gọi \((H): \frac{x^{2}}{25}-\frac{y^{2}}{16}=1\)
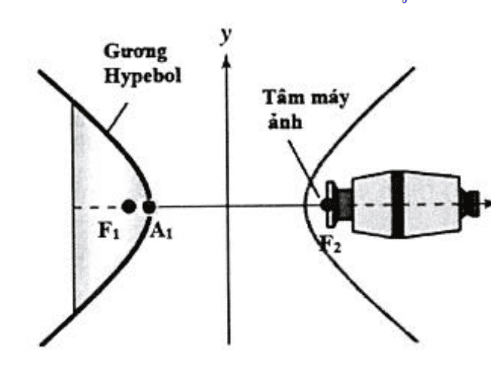
\(\Rightarrow\left\{\begin{array} { l } { a ^ { 2 } = 2 5 } \\{ b ^ { 2 } = 1 6 }\end{array} \Rightarrow \left\{\begin{array}{l}a=5 \\b=4\end{array} \Rightarrow c=\sqrt{a^{2}+b^{2}}=\sqrt{39}\right.\right. \text {. }\)Tiêu điểm của gương là \(F_{1}(-\sqrt{39} ; 0)\) và \(F_{2}(\sqrt{39} ; 0)\).
Đỉnh của gương là \(A_{1}(-5 ; 0)\).
Vậy khoảng cách từ tâm của máy ảnh tới đỉnh của gương là
\(F_{2} A_{1}=\sqrt{(-5-\sqrt{39})^{2}}=5+\sqrt{39} \text {. }\)Câu hỏi này nằm trong: