Cho hình hộp \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) có cạnh \(A B=a\) và diện tích tứ giác \(A^{\prime} B^{\prime} C D\) là \(2 a^{2}\). Mặt phẳng \(A^{\prime} B^{\prime} C D\) tạo với mặt phẳng đáy góc \(60^{\circ}\), khoảng cách giữa hai đường thẳng \(A A^{\prime}\) và \(C D\) bằng \(\frac{3 a \sqrt{21}}{7}\). Tính thể tích \(V\) của khối hộp đã cho, biết hình chiếu của \(A^{\prime}\) thuộc miền giữa hai đường thẳng \(A B\) và \(C D\), đồng thời khoảng cách giữa hai đường thẳng \(A B\) và \(C D\) nhỏ hơn \(4 a\).
A.
\(V=\sqrt{3} a^{3}\)
B.
\(V=3 \sqrt{3} a^{3}\)
C.
\(V=2 \sqrt{3} a^{3}\).
D.
\(6 \sqrt{3} a^{3}\).
Giải thích:
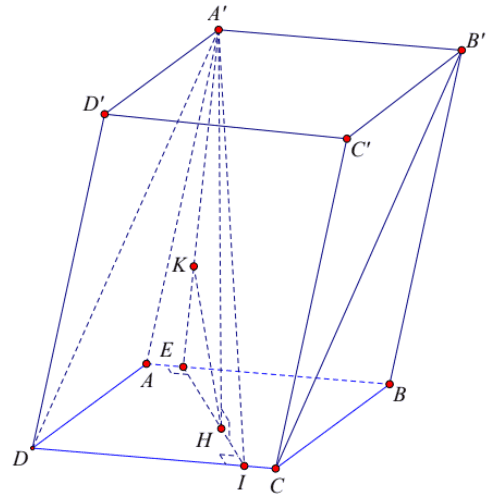
Gọi \(H\) là hình chiếu của \(A^{\prime}\) trên mặt phẳng \(A B C D, I, E\) lần lượt là hình chiếu của \(H\) trên \(C D\) và \(A B\). \(K\) là hình chiếu của \(H\) trên \(A^{\prime} E\). Khi đó \(A^{\prime} B^{\prime} C D ; A B C D=A^{\prime} I H=60^{\circ}\)
\(S_{A^{\prime} B^{\prime} C D}=A^{\prime} I \cdot C D=2 a^{2} \Rightarrow A^{\prime} I=\frac{2 a^{2}}{a}=2 a\)
\(I H=A^{\prime} I \cdot \cos 60^{\circ}=a ; A^{\prime} H=A^{\prime} I \cdot \sin 60^{\circ}=a \sqrt{3}\)
\(d A A^{\prime} ; C D=d C D ; A^{\prime} A B=d I ; A^{\prime} A B=\frac{3 a \sqrt{21}}{7}\)
Đặt \(E I=x, 0\lt x\lt 4 a\), ta có \(H K=d H, A^{\prime} A B=\frac{E H}{E I} d I, A^{\prime} A B=\frac{x-a}{x} \cdot \frac{3 a \sqrt{21}}{7}\)
Mặt khác
\(\frac{1}{H K^{2}}=\frac{1}{H E^{2}}+\frac{1}{H A^{\prime 2}} \Leftrightarrow \frac{1}{\frac{27 a^{2}}{7} \frac{x-a^{2}}{x^{2}}}=\frac{1}{x-a^{2}}+\frac{1}{3 a^{2}} \Leftrightarrow x^{2}-9 a x+18 a^{2}=0 \Leftrightarrow\left[\begin{array}{l}x=6 a(L) \\x=3 a(T M)\end{array}\right.\)Suy ra \(S_{A B C D}=E I \cdot A B=3 a^{2}\). Vậy \(V=3 a^{2} \cdot a \sqrt{3}=3 a^{3} \sqrt{3}\)
Câu hỏi này nằm trong: