Trong mặt phẳng tọa độ \(O x y\), cho tam giác \(A B C\) cân tại \(A\) biết đỉnh \(A(6 ; 6)\). Đường thẳng \(d\) đi qua trung điểm các cạnh \(A B, A C\) có phương trình \(x+y-4=0\). Biết điểm \(E(1 ;-3)\) thuộc đường cao đi qua đỉnh \(C\) của tam giác \(A B C\). Giả sử \(C\left(x_{C} ; y_{C}\right)\) và \(x_{C}\gt 0\). Tính \(x_{C}^{2}+y_{C}^{2}\).
Giải thích:
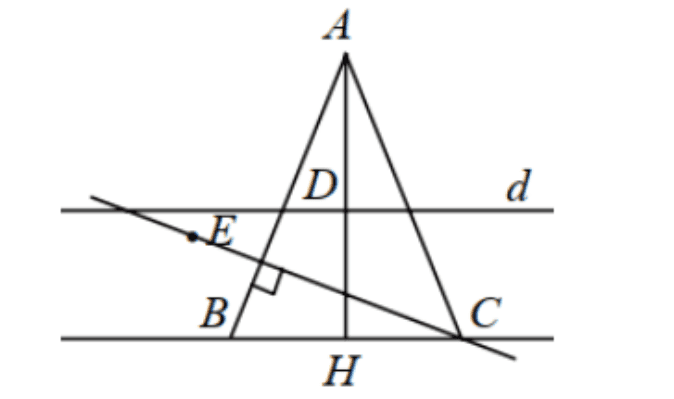
Ta có: \(A H \perp d \Rightarrow\) phương trình đường thẳng \(A H: x-y=0\).
Gọi \(H, D\) lần lượt là trung điểm của \(B C, A H\).
Toạ độ \(D\) là nghiệm của hệ: \(\left\{\begin{array}{l}x+y-4=0 \\ x-y=0\end{array} \Leftrightarrow x=y=2\right.\). Vậy \(D(2 ; 2) \Rightarrow H(-2 ;-2)\).
Do \(B C / / d \Rightarrow B C\) có phương trình: \(x+y+4=0\).\(C \in B C \Rightarrow C(t ;-t-4)\) với \(t\gt 0\).
Do \(H\) là trung điểm \(B C\) nên suy ra \(B(-t-4 ; t)\).
Ta có \(\overrightarrow{A B} \cdot \overrightarrow{C E}=0 \Leftrightarrow t^{2}+2 t-8=0 \Rightarrow t=2\) (do \(t>0\) ).
Vậy \(C(2 ;-6)\) nên \(x_{C}^{2}+y_{C}^{2}=2^{2}+(-6)^{2}=40\).
Câu hỏi này nằm trong: