Cho hai cây cột có chiều cao lần lượt là \(3 \mathrm{m}, 5 \mathrm{m}\) và được đặt cách nhau \(6\mathrm{m}\) . Một sợi dây dài được gắn vào đỉnh của mỗi cột và được đóng cọc xuống đất tại một điểm ở giữa hai cột. Chiều dài sợi dây được sử dụng ít nhất là bao nhiêu?
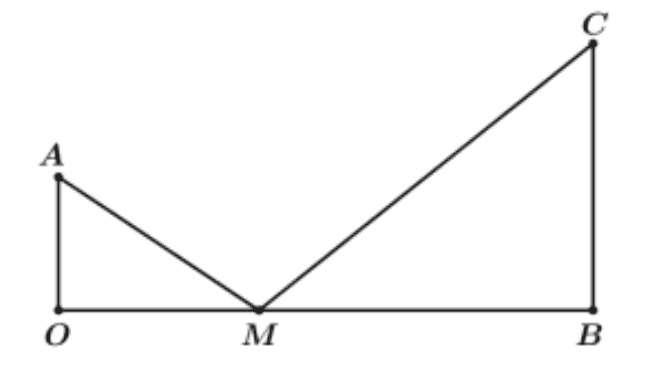
Giải thích:
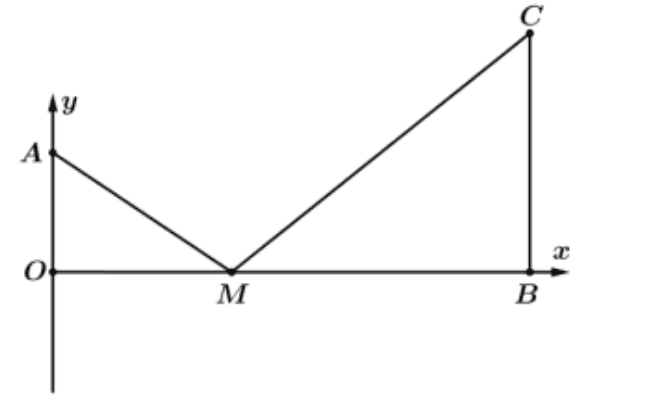
Lập hệ trục \(O x y\) như hình vẽ. Đặt \(A(0 ; 3), B(6 ; 0), C(6 ; 5)\).
Gọi \(D\) là điểm đối xứng của \(A\) qua \(O\), khi đó \(D(0 ;-3)\). Suy ra \(C D=\sqrt{(6-0)^{2}+(5+3)^{2}}=10\)
Ta có \(A M+M C=M D+M C \geq C D=10\).
Vậy độ dài sợi dây ngắn nhất là \(10\mathrm{m}\) .
Câu hỏi này nằm trong: