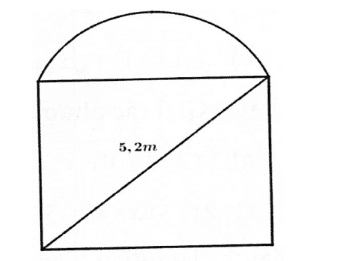
Ông An muốn làm cái cửa bằng nhôm có dạng nửa hình tròn ở phía trên và phía dưới có dạng hình chữ nhật như hình vẽ. Biết rằng đường kính của nửa hình nửa hình tròn cũng là cạnh phía trên của hình chữ nhật và đường chéo của hình chữ nhật có độ dài 5,2 mét; diện tích của nửa hình tròn bằng \(\frac{3}{10}\) diện tích của phần hình chữ nhật.
Tính số tiền ông An phải trả cho biết \(1 m^{2}\) cửa có giá 1300000 đồng (kết quả lấy gần đúng đến hàng phần mười).
Giải thích:
Gọi \(x(m)(x\gt 0)\) là đường kính của nửa đường tròn.
Khi đó hình chữ nhật có hai kích thước là \(x\) và \(\sqrt{5,2^{2}-x^{2}}\).
Diện tích nửa hình tròn là \(\frac{\pi x^{2}}{8}\) và diện tích hình chữ nhật là \(x \sqrt{5,2^{2}-x^{2}}\).
Theo giả thiết ta có: \(\frac{\pi x^{2}}{8}=\frac{3}{10} x \sqrt{5,2^{2}-x^{2}} \Leftrightarrow \frac{5}{12} \pi x=\sqrt{5,2^{2}-x^{2}}\)
\( \Leftrightarrow \frac{25}{144} \pi^{2} x^{2}=\frac{676}{25}-x^{2} \Leftrightarrow x^{2}\left(\frac{25}{144} \pi^{2}+1\right)=\frac{676}{25} \Leftrightarrow x \approx 3,2(m) \text {. }\)
Diện tích cánh cửa là: \(\frac{\pi \cdot 3,2^{2}}{8}+3,2 \sqrt{5,2^{2}-3,2^{2}} \approx 17,1\left(m^{2}\right)\).
Do đó số tiên ông An phải trả là: \(1300000 \cdot 17,1=22230000\) (đồng).
Câu hỏi này nằm trong: