Cho hình chóp \(S . A B C D\) có đáy \(A B C D\) là hình bình hành tâm \(O\). Gọi \(M\) là điểm nằm trên cạnh \(S C\) sao cho \(S M=\frac{1}{4} S C\).
1) Tim giao tuyến của hai mặt phẳng \((M B D)\) và \((S A C)\)
Giải thích:
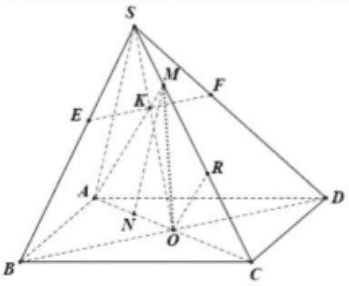
\(\begin{array}{l}\text { Ta có: } M \in S C \subset(S A C) \Rightarrow M \in(S A C) \Rightarrow M \in(M B D) \cap(S A C)(1) \\ \text { Lại có } O \in B D \subset(M B D) \Rightarrow O \in(M B D) \\ \quad O \in A C \subset(S A C) \Rightarrow O \in(S A C) \text { Suy ra } O \in(M B D) \cap(S A C)(2) \\ \text { Từ (1) và (2), suy ra } O M=(M B D) \cap(S A C)\end{array}\)
Câu hỏi này nằm trong: