Kim tự tháp Kheops ở Ai Cập có dạng hình chóp tứ giác đều có cạnh đáy dài 262 mét, cạnh bên dài 230 mét? Tính chiều cao kim tự tháp đó?

Giải thích:
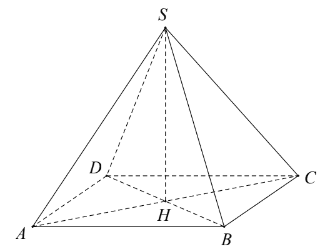
Ta giả sử các cạnh và đỉnh của kim tự tháp như hình vẽ.
Vì \(S . A B C D\) hình chóp tứ giác đều nên \(S H\) vuông góc với mặt phẳng \((A B C D) .(H=A C \cap B D)\)
Xét \(\triangle \mathrm{ABC}\) vuông tại \(B\), ta có: \(A C=\sqrt{A B^{2}+B C^{2}}=\sqrt{262^{2}+262^{2}}=262 \sqrt{2}(\mathrm{~m})\)
\(\Rightarrow H C=\frac{A C}{2}=131 \sqrt{2}(\mathrm{~m})\)
Xét \(\triangle\) SHC vuông tại \(H\), ta có: \(S H=\sqrt{S C^{2}-H C^{2}}=\sqrt{230^{2}-(131 \sqrt{2})^{2}}=\sqrt{18578} \approx 136(\mathrm{~m})\).
Vậy chiều cao của kim tự tháp là khoảng 136 mét.
Câu hỏi này nằm trong: