Cho hình lăng trụ đều \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\) có \(A B=\sqrt{3}\) và \(A A^{\prime}=1\). Góc tạo bởi giữa đường thẳng \(A C^{\prime}\) và \((A B C)\) bằng
A.
\(45^{\circ}\).
B.
\(60^{\circ}\)
C.
\(30^{\circ}\).
D.
\(75^{\circ}\).
Giải thích:
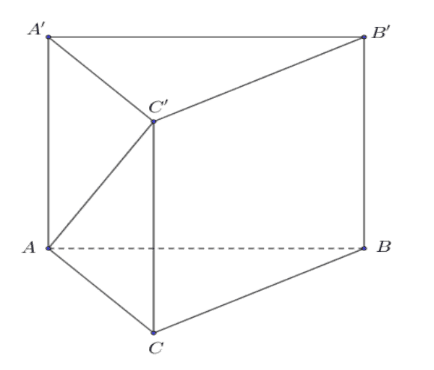
Ta có \(\left(\widehat{\left.A C^{\prime},(A B C)\right)}=\left(\widehat {\left.A C^{\prime}, A C\right)}=\widehat{C A C^{\prime}}, \tan \widehat{C^{\prime} A C}=\frac{C C^{\prime}}{A C}=\frac{1}{\sqrt{3}} \Rightarrow \widehat{C^{\prime} A C}=30^{\circ}\right.\right.\).
Câu hỏi này nằm trong: