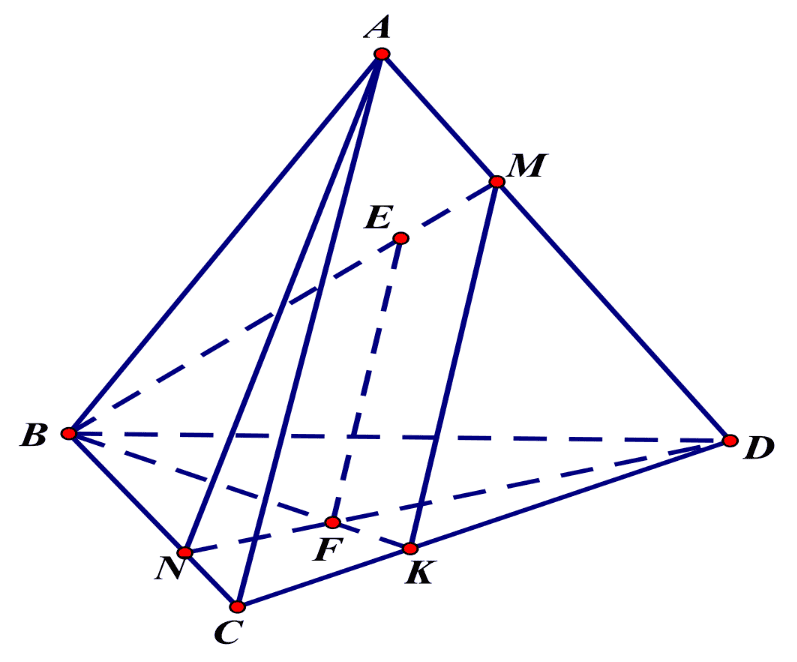
Qua \(\mathrm{M}\) kẻ đường thẳng song song với \(\mathrm{AC}\) cắt \(\mathrm{CD}\) tại \(\mathrm{K}\)

Ta có \(\mathrm{AC} / /(\mathrm{BMK})\) mà \(\mathrm{E}\) thuộc \((\mathrm{BMK})\) và \(\mathrm{EF} / / \mathrm{AC}\) nên \(\mathrm{EF}\) nằm trong \(\mathrm{mp}(\mathrm{BMK})\), do đó \(\mathrm{F}\) là giao điểm của \(\mathrm{DN}\) và \((\mathrm{BMK}) \Rightarrow F=B K \cap D N\)

Trong \(\mathrm{mp}(\mathrm{BKM})\), từ \(\mathrm{F}\) kẻ đường thẳng song với \(\mathrm{MK}\) cắt \(\mathrm{BM}\) tại \(\mathrm{E}\)

Ta có hai điểm \(\mathrm{E}, \mathrm{F}\) cần tìm

Do \(\frac{A M}{\mathrm{MD}}=\frac{C K}{K D}=\frac{1}{2}=\frac{C N}{N B}\) nên \(\mathrm{NK} / / \mathrm{BD}\)

Suy ra \(\frac{K F}{F B}=\frac{N K}{B \mathrm{D}}=\frac{C K}{C \mathrm{D}}=\frac{1}{3}\)

\(\Rightarrow \frac{E F}{M K}=\frac{B F}{B K}=\frac{3}{4}\) mà \(\frac{M K}{A C}=\frac{2}{3}\)

Do đó \(\frac{E F}{A C}=\frac{E F}{M K} \cdot \frac{M K}{A C}=\frac{3}{4} \cdot \frac{2}{3}=\frac{1}{2}\)