Một vật chuyển động có vận tốc (mét/giây) được biểu diễn theo thời gian \(t\) (giây) bằng công thức \(v(t)=\frac{1}{2} t^{2}-4 t+10\).
b) Trong 10 giây đầu tiên, vận tốc của vật đạt giá trị nhỏ nhất bằng bao nhiêu?
Giải thích:
Xét \(v(t)=\frac{1}{2} t^{2}-4 t+10\) với \(-\frac{b}{2 a}=4, a=\frac{1}{2}\gt 0\) nên bề lõm parabol hướng lên. Bảng biến thiên của \(v(t)\) :
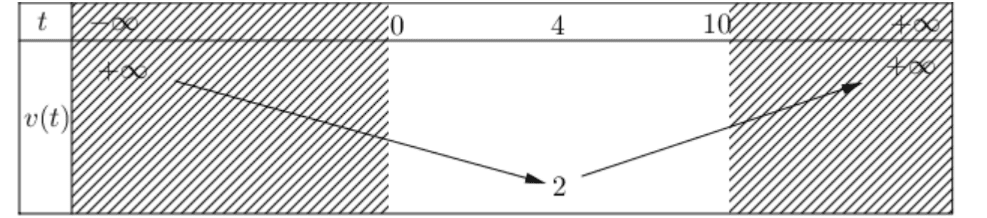
Vậy, ở giây thứ tư thì vận tốc của vật đạt giá trị nhỏ nhất là \(v(t)_{\min }=2\).
Câu hỏi này nằm trong: