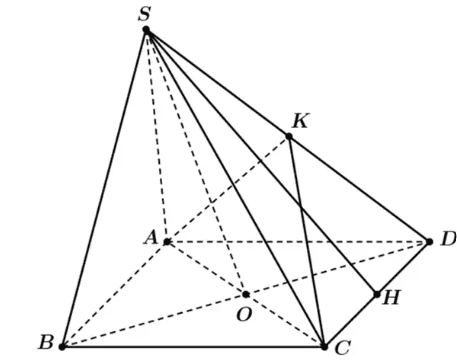
Gọi \(O\) là giao điểm của \(C\) và \(B D\).

Vì \(A B C D\) là hình vuông nên \(O A=O B=O C=O D\), suy ra \(O\) là tâm đường tròn ngoại tiếp \(A B C D\) nên \(O\) là chân đường cao của khối chóp \(S . A B C D\).

Khi đó, chiều cao của khối chóp \(S.A B C D\) bằng \(S O\).

Trong hình vuông \(A B C D\), ta có:\(A O=\frac{1}{2} A C=\frac{1}{2} \sqrt{A B^{2}+B C^{2}}=\frac{1}{2} \sqrt{a^{2}+a^{2}}=\frac{a \sqrt{2}}{2}\).

Xét tam giác SAO vuông tại \(O\) có: \(S O=\sqrt{S A^{2}-A O^{2}}=\sqrt{\left(\frac{a \sqrt{6}}{3}\right)^{2}-\left(\frac{a \sqrt{2}}{2}\right)^{2}}=\frac{a \sqrt{6}}{6}\)

Vậy chiều cao cua khối chóp \(S . A B C D\) bằng \(\frac{a \sqrt{6}}{6}\).