Cho hình chóp \(S \cdot A B C D\) có đáy \(A B C D\) là hình vuông cạnh \(a\), tâm \(O\). Cạnh bên \(S A\) vuông góc với \((A B C D)\) và có độ dài là \(x\).
a) Biết góc giữa đường thẳng \(S C\) và \((A B C D)\) bằng \(60^{\circ}\). Khi đó \(\mathrm{x}=\mathrm{a} \sqrt{6}\).
A.
True
B.
False
Giải thích:
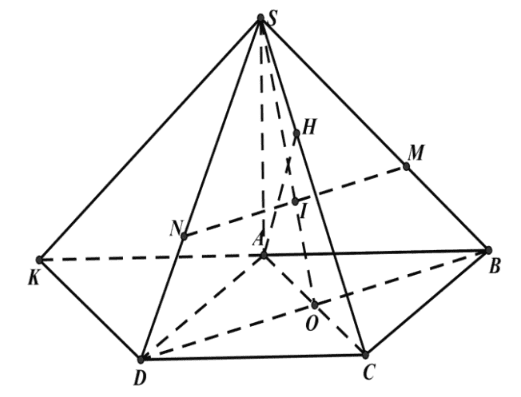
Do \(S A\) vuông góc \((A B C D)\) nên hình chiếu của \(S C\) trên \((A B C D)\) là \(A C\).
Khi đó góc giữa \(S C\) và \((A B C D)\) là góc giữa hai đường thẳng \(S C\) và \(A C\), và chính là góc \(S C A\).
Suy ra \(\widehat {S C A}=60^{\circ}\)Trong tam giác vuông \(A S C \cdot \tan 60^{\circ}=\frac{S A}{A C} \rightarrow x=A C \cdot \sqrt{3}=a \sqrt{6}\).
Câu hỏi này nằm trong: