Cho hình chóp $S . A B C D$ có đáy $A B C D$ là hình vuông cạnh bằng $a$. Mặt bên $S A B$ là tam giác đều nằm trong mặt phẳng vuông góc với đá...

Question

Accepted Answer

A.

$\frac{8}{3} \pi a^{2}$.

B.

$\frac{7}{3} \pi a^{2}$.

C.

$\frac{5}{3} \pi a^{2}$.

D.

$\frac{2}{3} \pi a^{2}$.

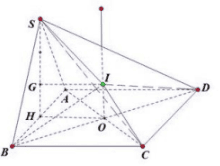
Gọi $H$ là trung diểm $A B \Rightarrow S H \perp(A B C D)$.

Gọi G là trọng tâm của $\triangle S A B$, kẻ $\Delta / / O H ; \Delta$ đi qua G.

Kẻ đường thẳng $d$ đi qua tâm $\mathrm{O}$ của $A B C D$ và $d / / S H$.

Vi $S H \perp(A B C D) ; d / / S H \Rightarrow d \perp(A B C D)$.

Gọi $I$ là giao điểm của $d$ và $\Delta$

Vi $O H \perp A B \Rightarrow G I \perp(S A B)$.Vì $I \in \Delta \Rightarrow I S=I A=I B$.

Vì $I \in d \Rightarrow I A=I B=I C=I D$.

Do đó: $I A=I B=I C=I D=I S$.$\Rightarrow I$ là tâm mặt cầu ngoại tiếp chóp $S . A B C D$.

Bán kính mặt cầu: $R=I S$.Ta có: $G I=O H=\frac{1}{2} A B=\frac{a}{2}$.

$S G=\frac{2}{3} S H=\frac{a \sqrt{3}}{2} \Rightarrow R=I S=\sqrt{S G^{2}+G I^{2}}=\frac{a \sqrt{21}}{6} \text {. }$

Vậy diện tích mặt cầu là $S=4 \pi R^{2}=4 \pi \cdot \frac{21}{36} a^{2}=\frac{7}{3} \pi a^{2}$.