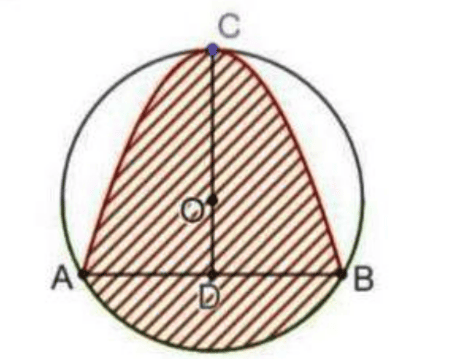
Một hoa văn hình tròn tâm \(O\), ngoại tiếp tam giác đều \(A B C\) có cạnh \(A B=4 \sqrt{3} \mathrm{~cm}\). Đường cong qua ba điểm: \(A, B, C\) là một phần của parabol. Diện tích phần gạch chéo bằng
A.
\(37,54 \mathrm{~cm}^{2}\)
B.
\(9,83 \mathrm{~cm}^{2}\)
C.
\(27,71 \mathrm{~cm}^{2}\).
D.
\(36,75 \mathrm{~cm}^{2}\).
Giải thích:
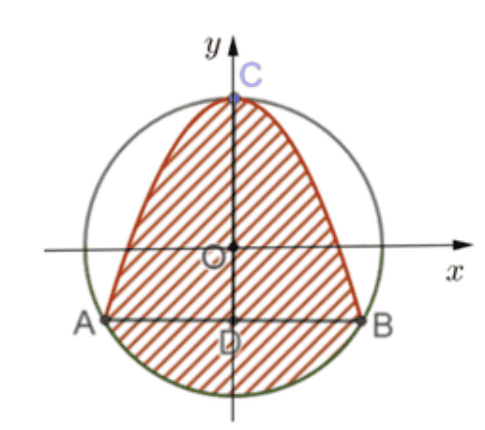
Do tam giác \(A B C\) là tam giác đều có cạnh \(4 \sqrt{3} \mathrm{~cm}\) nên \(C D=4 \sqrt{3} \cdot \frac{\sqrt{3}}{2}=6(\mathrm{~cm}) \Rightarrow O C=\frac{2}{3} C D=4(\mathrm{~cm})\) và \(O D=2(\mathrm{~cm})\).
Gắn trục tọa độ \(O x y\) như hình vẽ, ta có \(A(-2 \sqrt{3} ;-2), B(2 \sqrt{3} ;-2), C(0 ; 4)\)
Phương trình đường Parapol đi qua 3 điểm \(A, B, C\) có đỉnh \(C\) có dạng \(y=a x^{2}+4(P)\).
Thay tọa độ điểm \(B(2 \sqrt{3} ;-2)\) vào \((P)\) suy ra \(a=-\frac{1}{2} \Rightarrow(P): y=-\frac{1}{2} x^{2}+4\)
Phương trình đường tròn tâm \(O\) bán kính \(O A=4\) là \(x^{2}+y^{2}=16 \Rightarrow\) Phương trình một phần cung nhỏ \(A B\) có dạng \(y=-\sqrt{16-x^{2}}\)
Vậy diện tích phần gạch chéo bằng \(\int_{-2 \sqrt{3}}^{2 \sqrt{3}}\left[\left(-\frac{1}{2} x^{2}+4\right)-\left(-\sqrt{16-x^{2}}\right)\right] \approx 37,54\left(\mathrm{~cm}^{2}\right)\)
Câu hỏi này nằm trong: