Ta có \(e^{x}=\ln (x+2 m)+2 m \Leftrightarrow e^{x}+x=\ln (x+2 m)+x+2 m \Leftrightarrow e^{x}+x=e^{\ln (x+2 m)}+\ln (x+2 m)\ (^*)\)

Xét hàm số \(f(t)=e^{t}+t\) với \(t \in \mathbb{R} \Rightarrow f^{\prime}(t)=e^{t}+1\gt 0, \forall t\). Suy ra hàm số \(f(t)\) đồng biến trên \(\mathbb{R}\).

Do đó \(\left({ }^{*}\right) \Leftrightarrow f(x)=f(\ln (x+2 m)) \Leftrightarrow x=\ln (x+2 m) \Leftrightarrow x+2 m=e^{x} \Leftrightarrow 2 m=e^{x}-x\).

Xét hàm số \(g(x)=e^{x}-x \Rightarrow g^{\prime}(x)=e^{x}-1 \Rightarrow g^{\prime}(x)=0 \Leftrightarrow x=0\).

Bảng biên thiên

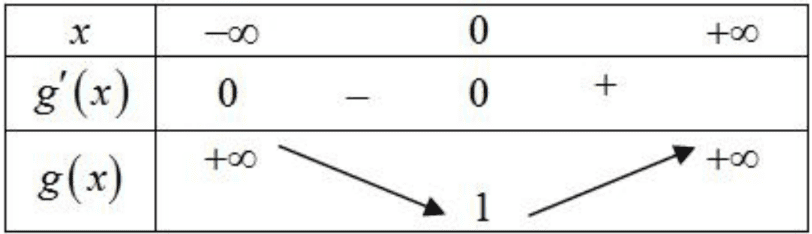
Từ bảng biên thiên suy ra phương trình có nghiệm khi và chỉ khi \(2 m \geq 1 \Leftrightarrow m \geq \frac{1}{2}\).

Mà \(m \in \mathbb{Z}, m \in(-2020 ; 2020)\) nên \(m \in\{1 ; 2 ; 3 ; \ldots ; 2019\}\).

Vậy có 2019 giá trị nguyên của tham số \(m\) thuộc \((-2020 ; 2020)\) để phương trình \(e^{x}=\ln (x+2 m)+2 m\) có nghiệm.