Cho khối chóp \(S . A B C\) có đáy \(A B C\) là tam giác vuông tại \(B, A B=a, A C=2 a, S A \perp(A B C)\) và \(S A=a\). Thể tích của khối chóp đã cho bằng
A.
\(\frac{a^{3} \sqrt{3}}{3}\)
B.
\(\frac{a^{3} \sqrt{3}}{6}\)
C.
\(\frac{a^{3}}{3}\)
D.
\(\frac{2 a^{3}}{3}\)
Giải thích:
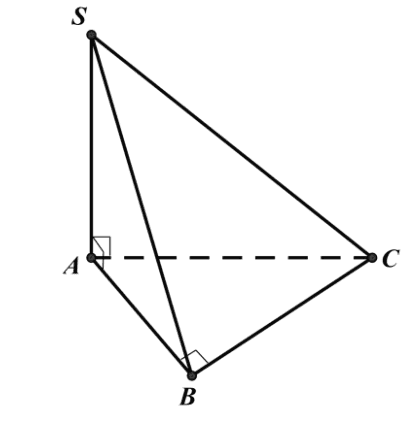
Xét tam giác \(A B C\) vuông tại \(B\) có: \(B C^{2}=A C^{2}-A B^{2}=(2 a)^{2}-a^{2}=3 a^{2} \Rightarrow B C=a \sqrt{3}\).
Diện tích tam giác \(A B C\) là: \(S_{\triangle A B C}=\frac{1}{2} B A \cdot B C=\frac{1}{2} a \cdot a \sqrt{3}=\frac{a^{2} \sqrt{3}}{2}\).
Vậy thể tích khối chóp \(S \cdot A B C\) là: \(V_{S \cdot A B C}=\frac{1}{3} S_{\triangle A B C} \cdot S A=\frac{1}{3} \cdot \frac{a^{2} \sqrt{3}}{2} \cdot a=\frac{a^{3} \sqrt{3}}{6}\).
Câu hỏi này nằm trong: