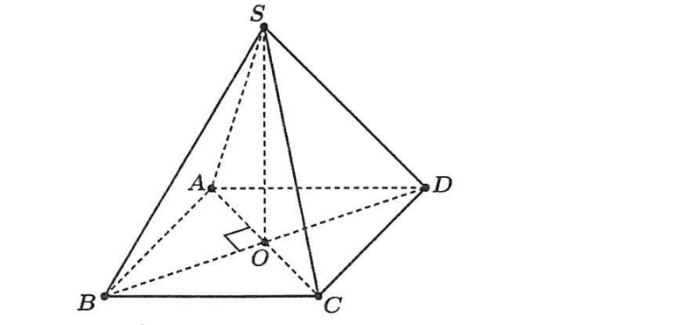
Cho hình chóp \(S \cdot A B C D\), đáy là hình thoi tâm \(O\) và \(S A=S C, S B=S D\). Khi đó:
a) \(S O \perp A C\)
A.
True
B.
False
Giải thích:
Tam giác \(S A C\) cân tại \(S\) (do \(S A=S C\) ), mà \(O\) là trung điểm \(A C\) nên \(S O \perp A C\). (1)
Tam giác \(S B D\) cân tại \(S\) (do \(S B=S D\) ), mà \(O\) là trung điểm \(B D\) nên \(S O \perp B D\). (2)
Từ (1) và (2) suy ra \(S O \perp(A B C D)\).
Ta có: \(\left\{\begin{array}{l}A C \perp B D \\ A C \perp S O(\text { do } S O \perp(A B C D)) \text { mà } S B \subset(S B D) \text { nên } A C \perp S B \text {. }\end{array}\right.\)
\(\Rightarrow A C \perp(S B D)\);
Câu hỏi này nằm trong: