Cho hình lập phương \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\). Góc giữa hai đường thẳng \(A^{\prime} C^{\prime}\) và \(B D\) bằng.
A.
\(60^{\circ}\)
B.
\(30^{\circ}\)
C.
\(45^{\circ}\)
D.
\(90^{\circ}\)
Giải thích:
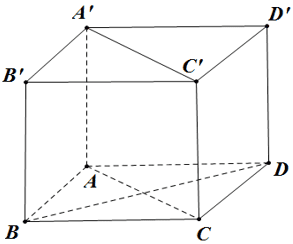
Ta có: \(\left(\widehat{A^{\prime} C^{\prime} ; B D}\right)=(\widehat{A C ; B D})=90^{\circ}\)
Câu hỏi này nằm trong: