Cho hộp chữ nhật \(A B C D \cdot A^{\prime} B C^{\prime} D^{\prime}\) có cạnh \(A B=a, A D=2 a ; A A^{\prime}=3 a\). Khoảng cách giữa đường thẳng \(B^{\prime} C^{\prime}\) và mặt phẳng \((A B C D)\) bằng
A.
\(a\)
B.
\(2 a\)
C.
\(3 a\)
D.
\(5 a\)
Giải thích:
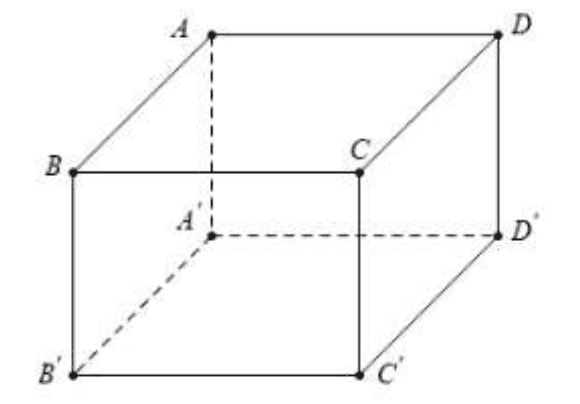
Ta có \(d\left(B^{\prime} C^{\prime} ;(A B C D)\right)=A A^{\prime}=3 a\).
Câu hỏi này nằm trong: