Cho tứ diện đều \(A B C D\) có cạnh bằng \(a, M\) là trung điểm cạnh \(B C, N\) là trung điểm của \(A C\). Khi đó:
d) \(\cos (A B, D M)=\frac{\sqrt{3}}{3}\)
A.
True
B.
False
Giải thích:
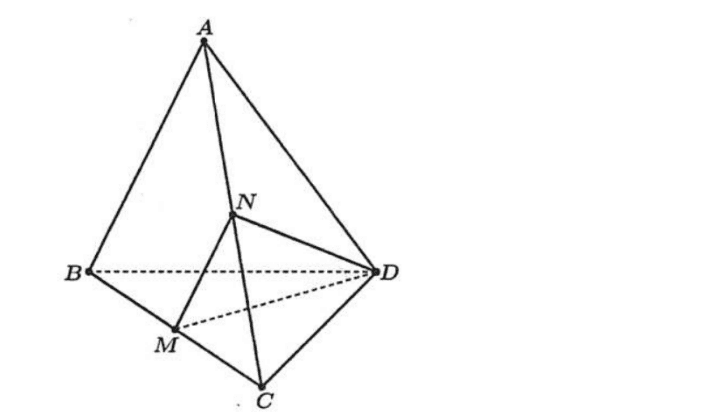
Gọi \(N\) là trung điểm của \(A C\) nên \(M N\) là đường trung bình của \(\triangle A B C\)
\[\Rightarrow\left\{\begin{array}{l}M N / / A B\left(^{*}\right) \\M N=\frac{1}{2} A B=\frac{a}{2}\end{array}\right.\]Vì \(\triangle B C D\) và \(\triangle A C D\) là các tam giác đều cạnh bằng \(a\) nên \(M D=N D=\frac{a \sqrt{3}}{2}\).
Từ \(\left({ }^{*}\right)\) suy ra: \((A B, D M)=(M N, D M)\).
Xét \(\triangle M N D\), ta có:
\[\cos \widehat{D M N}=\frac{M N^{2}+M D^{2}-N D^{2}}{2 M N \cdot M D}=\frac{\left(\frac{a}{2}\right)^{2}+\left(\frac{a \sqrt{3}}{2}\right)^{2}-\left(\frac{a \sqrt{3}}{2}\right)^{2}}{2 \cdot \frac{a}{2} \cdot \frac{a \sqrt{3}}{2}}=\frac{\sqrt{3}}{6}\gt 0\]\(\Rightarrow \widehat{D M N}\) là góc nhọn.
Vậy \((A B, D M)=(M N, D M)=\widehat{D M N}\) nên \(\cos (A B, D M)=\frac{\sqrt{3}}{6}\).
Câu hỏi này nằm trong: