Trong mặt phẳng $O x y$, cho điểm $M(2 ; 1)$ và đường tròn $(C):(x-1)^{2}+(y-2)^{2}=4$. Viết phương trình đường thẳng $d: a x+b y+c=0$ qua điể...

Question

Accepted Answer

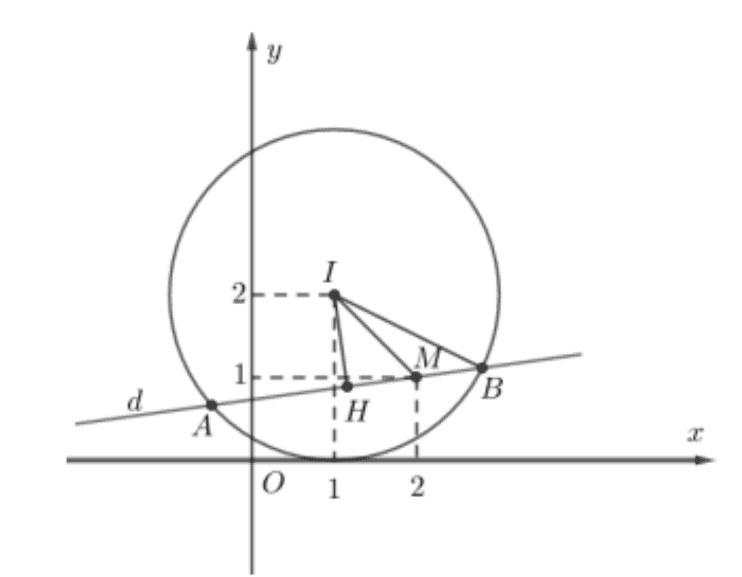
Đường tròn $(C)$ có tâm $I(1 ; 2)$, bán kính $R=2$.

Ta có: $I M=\sqrt{2}\lt R=2$ nên điểm $M$ nằm trong đường tròn.

Gọi $H$ là trung điểm của $A B$. Ta có $A B=2 H B=2 \cdot \sqrt{I B^{2}-I H^{2}}=2 \sqrt{4-I H^{2}}$

Vì $I H \leq I M=\sqrt{2}$ nên $A B=2 \sqrt{4-I H^{2}} \geq 2 \sqrt{4-I M^{2}}=2 \sqrt{2}$ do đó $A B$ ngắn nhất khi $I H=I M$

Lúc đó, đường thẳng $d$ qua $M(2 ; 1)$ và nhận $\overrightarrow{I M}=(1 ;-1)$ làm vectơ pháp tuyến

$\Rightarrow d: 1(x-2)-1(y-1)=0 \Leftrightarrow d:-x+y+1=0 \Rightarrow\left\{\begin{array}{l}a=-1 \ b=1 \ c=1\end{array} \Rightarrow a+b+c=1\right.$.