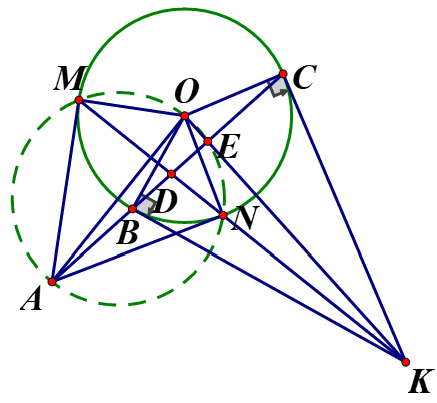
Gọi \(K M\) cắt \((\mathrm{O})\) tại \(N^{\prime}\)

Vì tứ giác \(M B N^{\prime} C\) nội tiếp \(\Rightarrow \triangle K B N^{\prime}\sim\triangle K M B \Rightarrow K N^{\prime} \cdot K M=K B^{2}\)

Gọi \(K O\) cắt \(B C\) tại \(E\)

Dễ thấy \(\angle O E A=90^{\circ}=\angle O N A=\angle O M A \Rightarrow 5\) điểm \(O, M, N, E, A\) cùng thuộc một đường tròn (1)

Áp dụng hệ thức lượng trong \(\triangle K B O\) vuông tại \(\mathrm{B}\), đường cao \(B E\), ta có:\(K E \cdot K O=K B^{2}=K N^{\prime} \cdot K M \Rightarrow \triangle K N^{\prime} E \sim\triangle K O M\)\(\Rightarrow \angle O M^{\prime} N=\angle O M K=\angle N^{\prime} E K=180^{\circ}-\angle OE N^{\prime} \Rightarrow \angle O M N^{\prime}+\angle O E N^{\prime}=180^{\circ}\)

\(\Rightarrow\) Tứ giác \(M O E N\) 'nội tiếp hay 5 điểm \(M, O, E, N^{\prime},A\) cùng thuộc một đường tròn, kết hợp với (1) suy ra \(N \equiv N'\)hay \(K \in M N\) cố định